一文详解卷积和逆卷积
卷积神经网络(CNN)在计算机视觉大放异彩,入门CNN的第一步就是理解什么是卷积(Convolution)运算。本文旨在以通俗易懂的方式让读者理解卷积的概念。
注:本文的图片素材全部来源于网络,如有侵权,请联系作者删除。
卷积运算
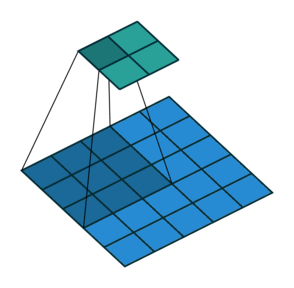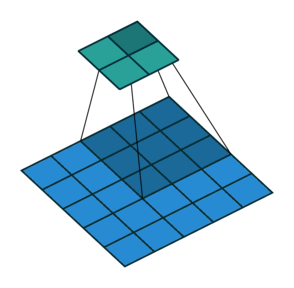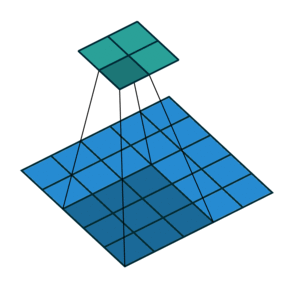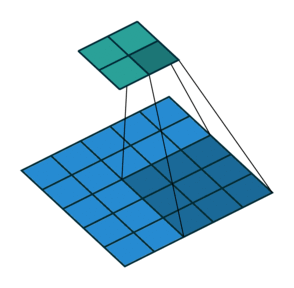
卷积在数学上是两个变量在某范围内相乘后求和的结果。在数字图像处理中,卷积操作其实就是利用卷积核(卷积模板)在图像上滑动,将图像点上的像素灰度值与对应的卷积核上的数值相乘,然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值,并最终滑动完所有图像的过程,如图下图所示(图中的蓝色代表输入,青色代表输出)。
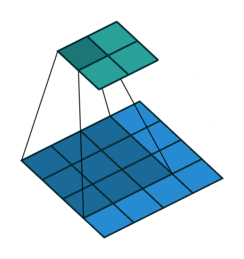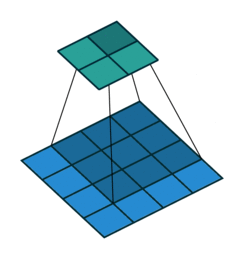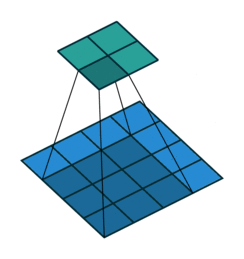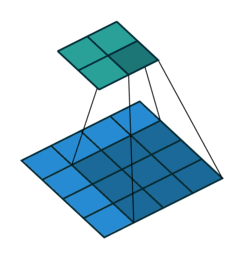
在卷积运算中,我们有下面几个概念:
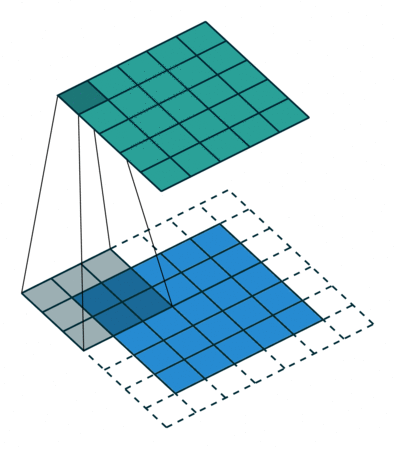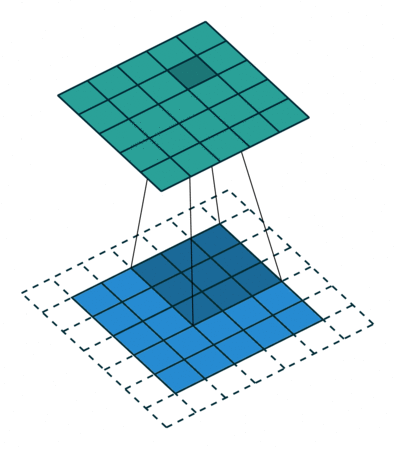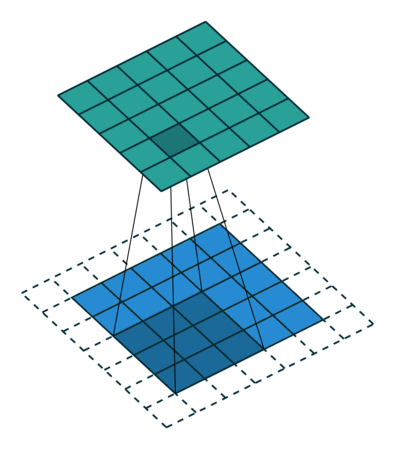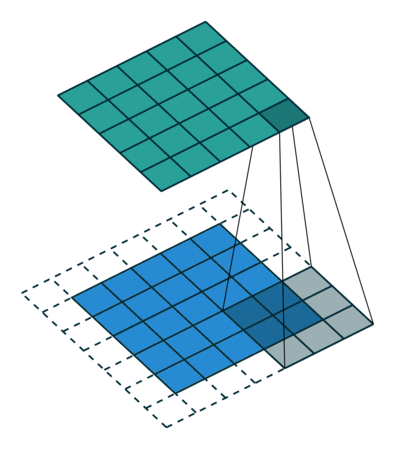
- Padding 有的时候对于给定输入图像的大小,我们需要得到制定大小的输出。这时候,我们可以通过给图像的边缘增加0像素值得方法获得。这个0像素值区域的大小,我们一般称之为padding。
- Stride 在一般的卷积过程中,我们使用步长为1进行卷积核在图像上的滑动;但是有时候出于缩小输出图片尺寸的原因,我们也会采用大于1的步长。卷积核每次滑动的步长,我们称之为stride。
 |
 |
|---|---|
| Padding为$1\times1$的卷积操作 | Stride为$2\times2$的卷积操作 |
单通道
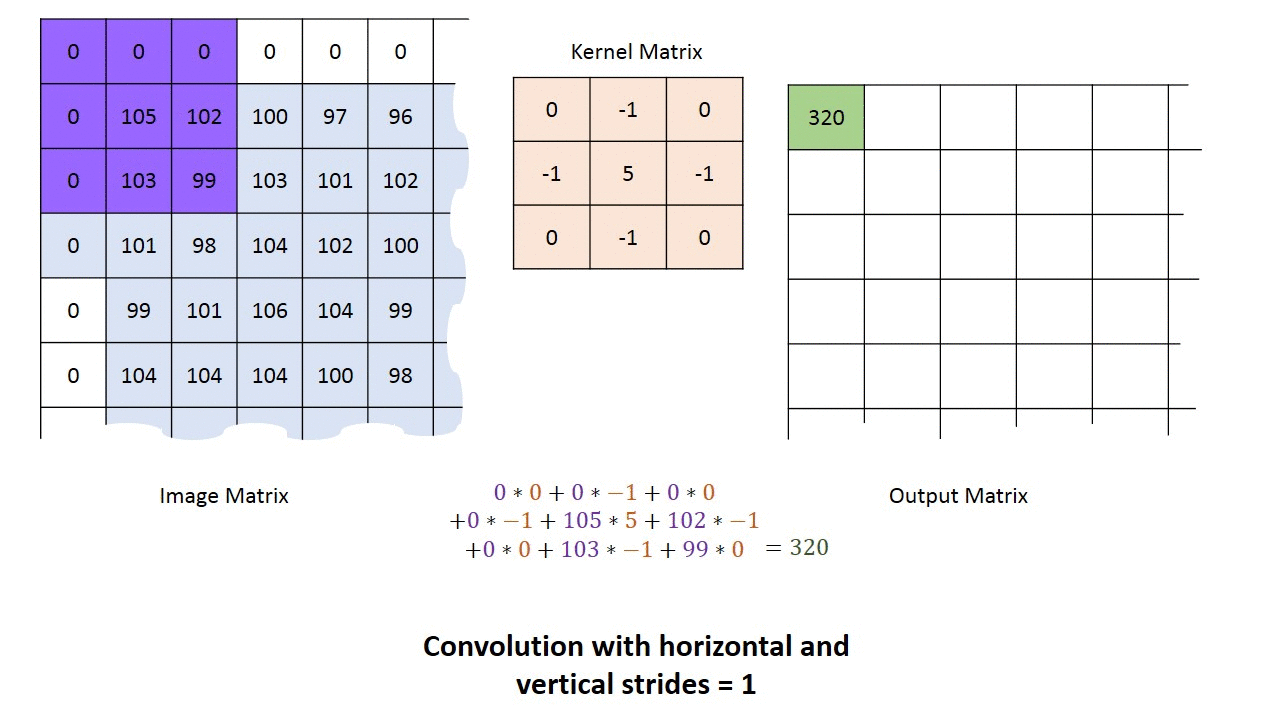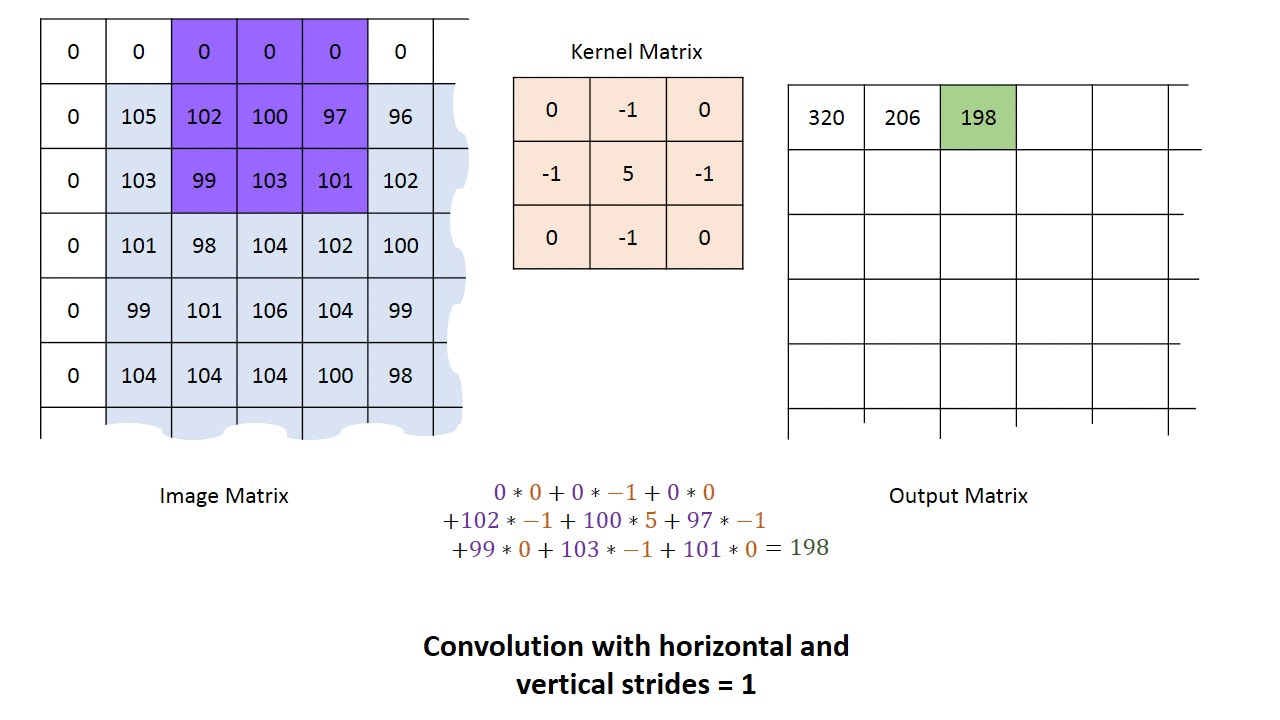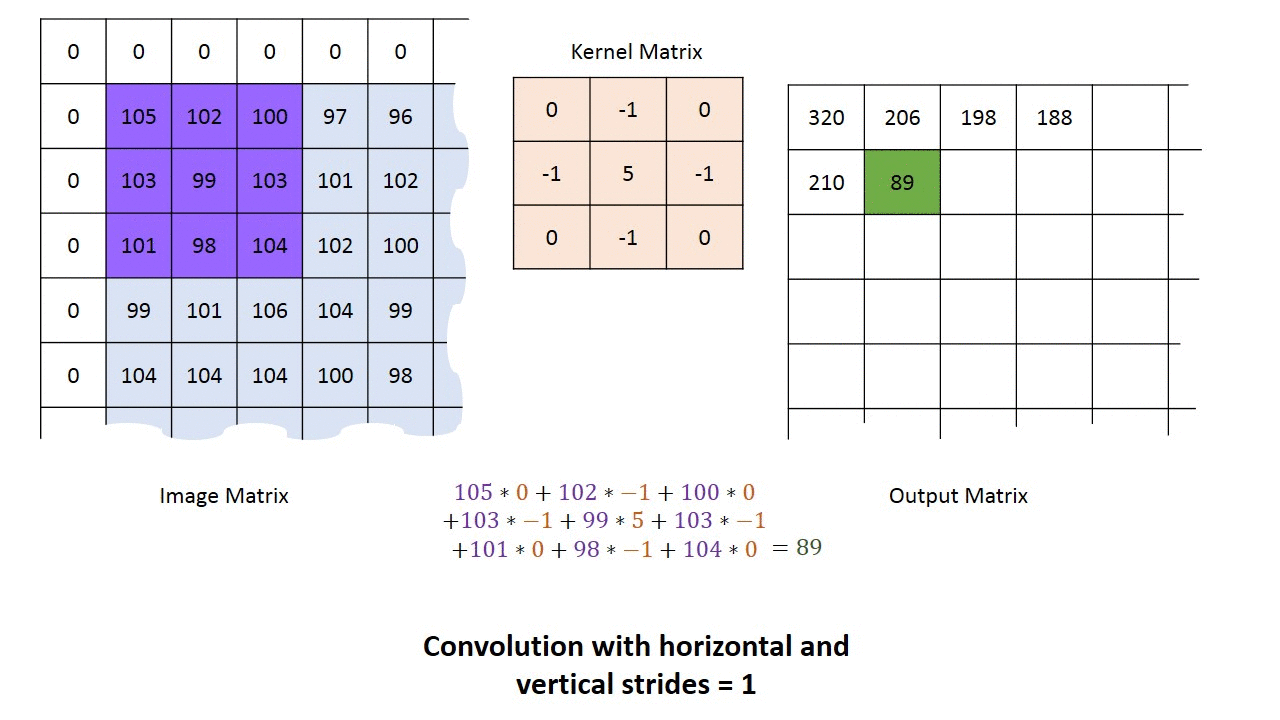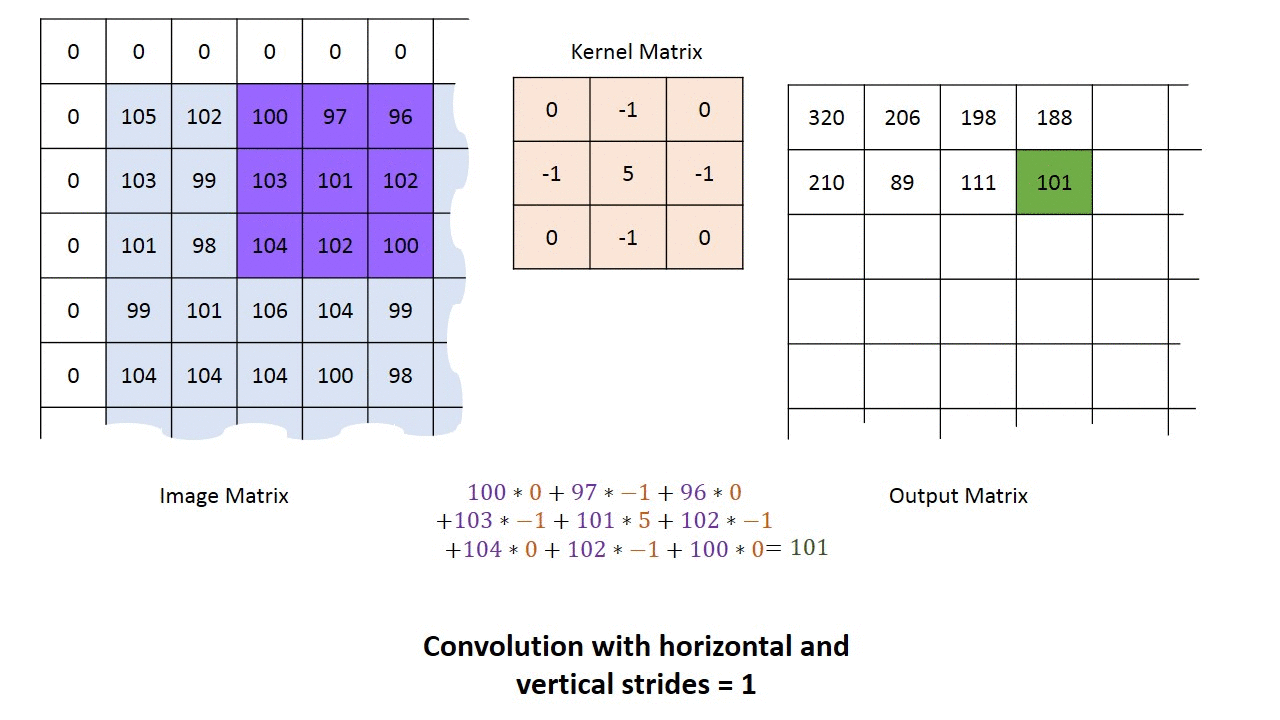
对于一个长为$H$,宽为$W$的灰度图像来说,其尺寸可以表示为$(1, W, H)$。这里的1我们称之为通道(Channel)。所谓“一图胜千言”,下面的动图以单通道为例,演示了如何进行卷积运算得到最终的输出结果。
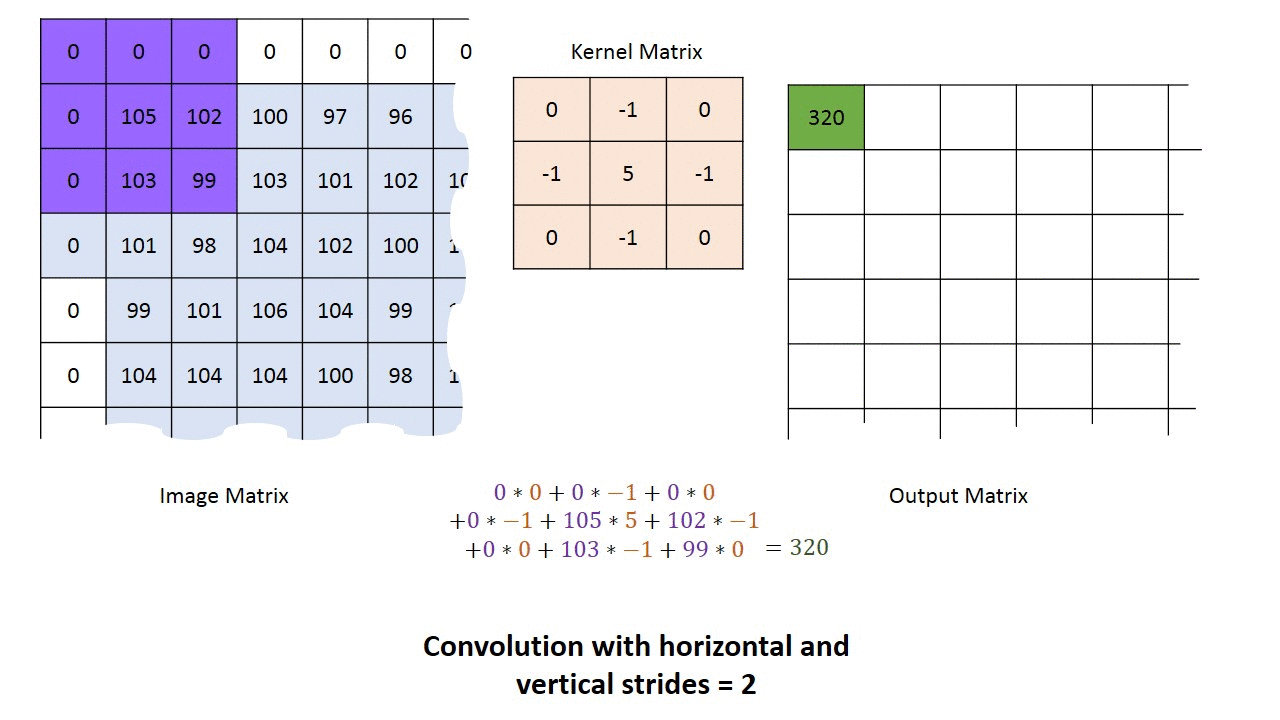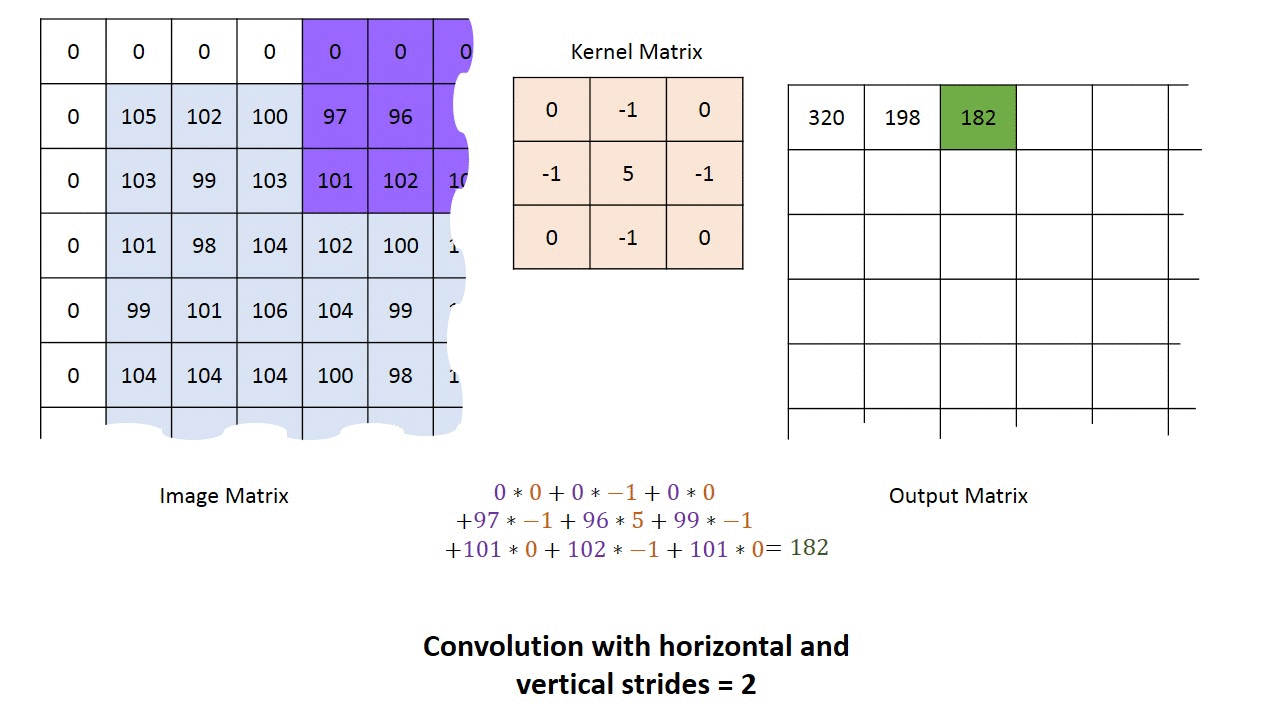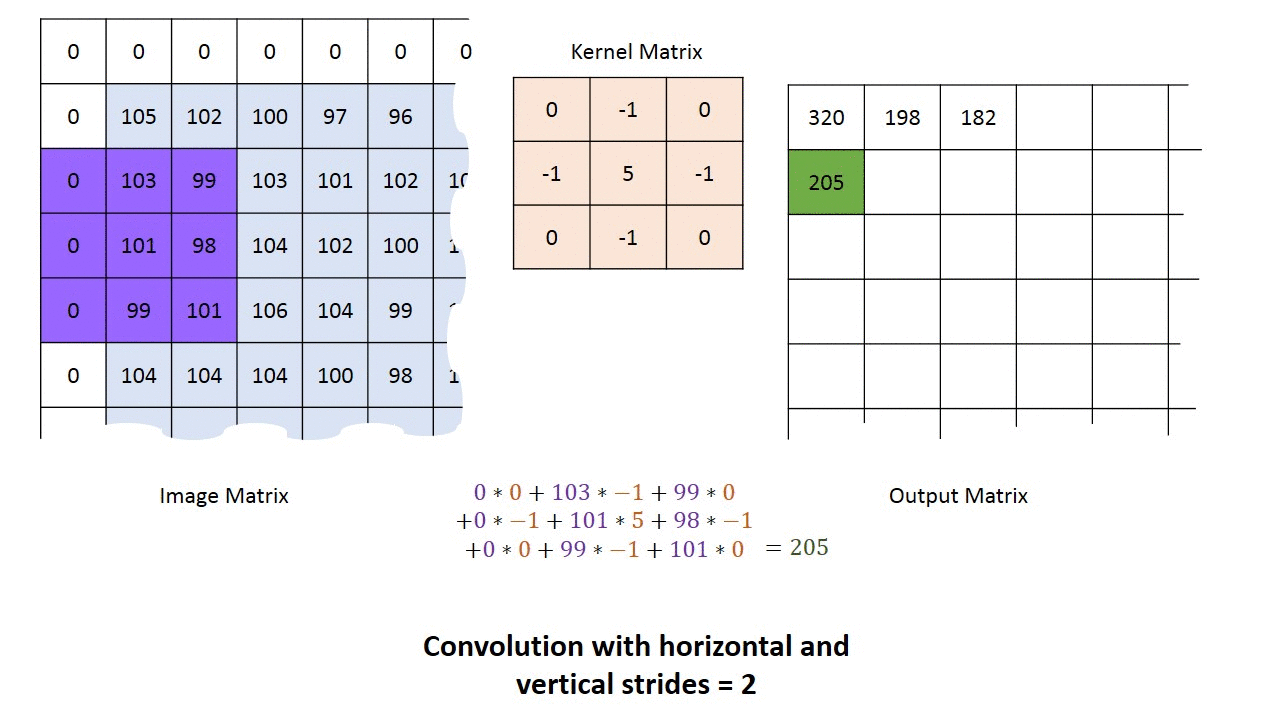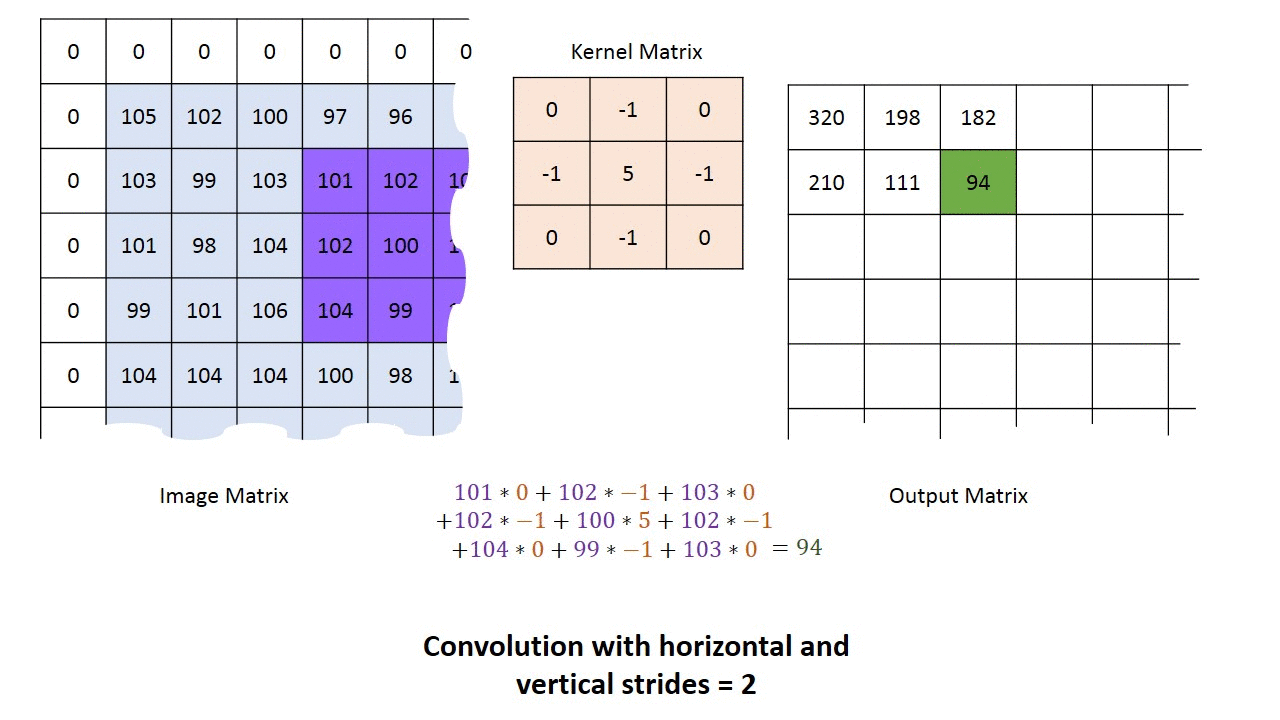
多通道
那如果对于一个RGB彩色图像我们的通道就是3,对于多通道的输入,我们如何进行卷积操作,输出为多通道或者单通道呢?
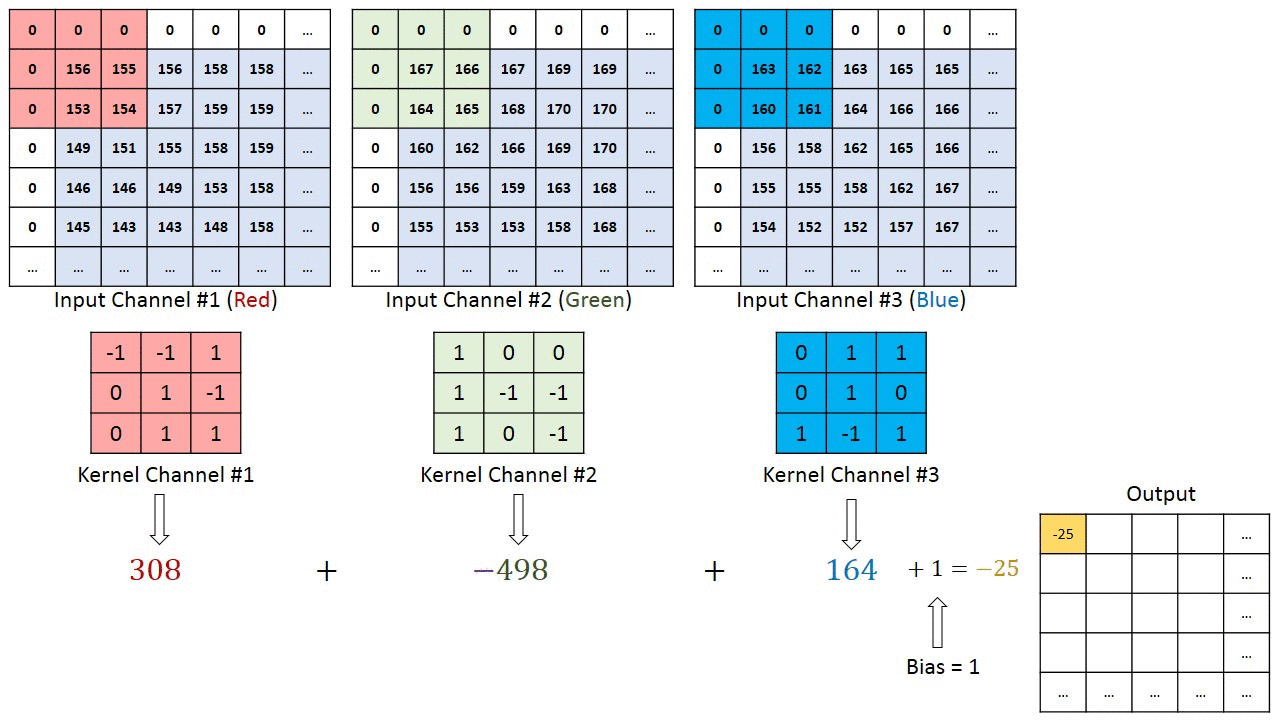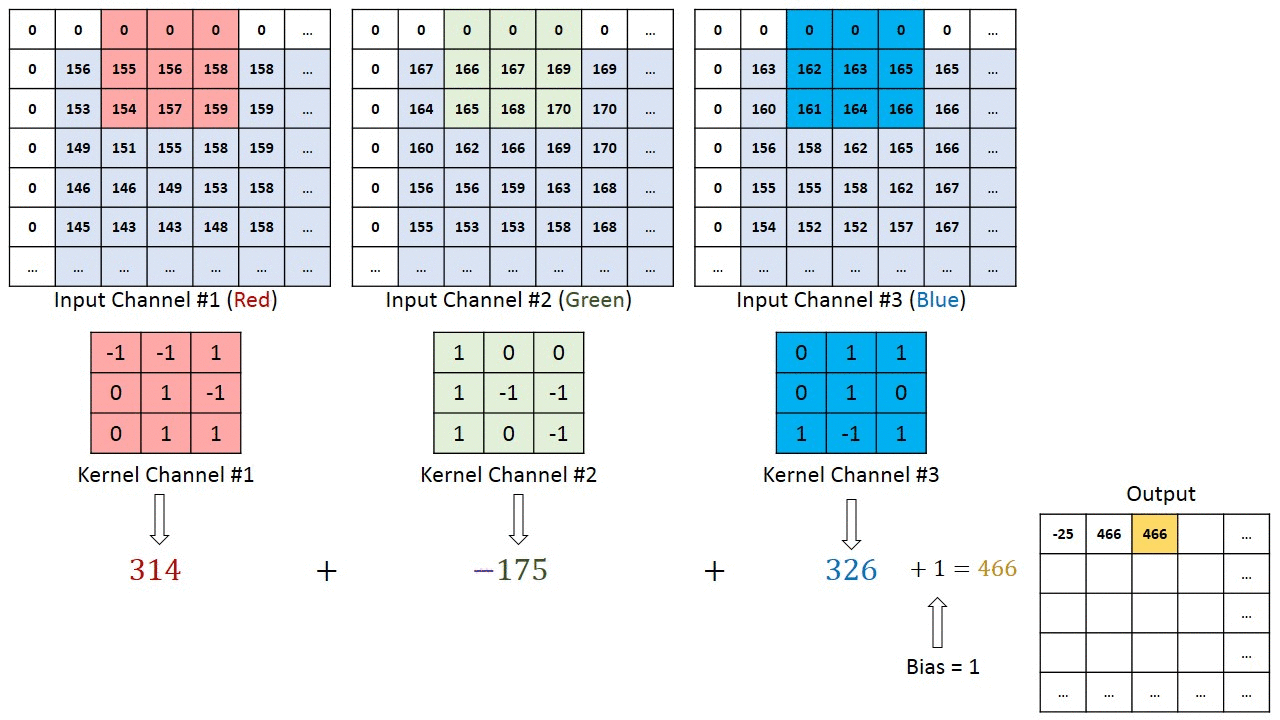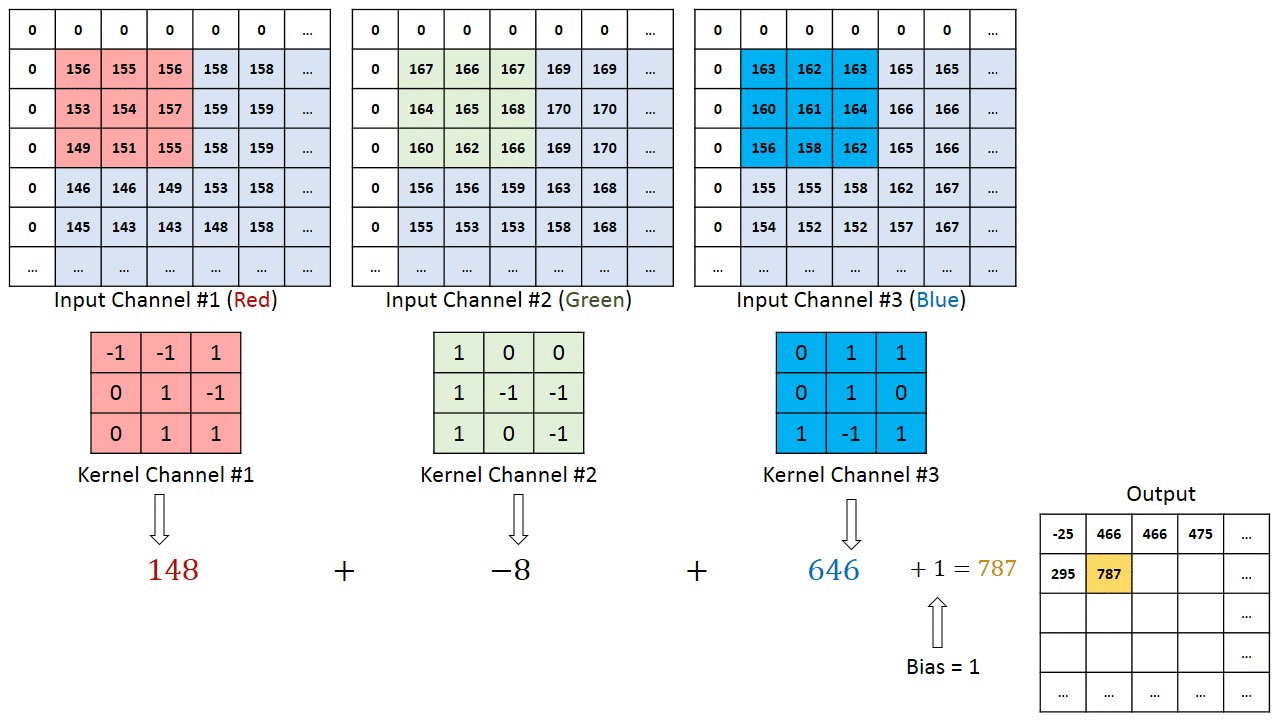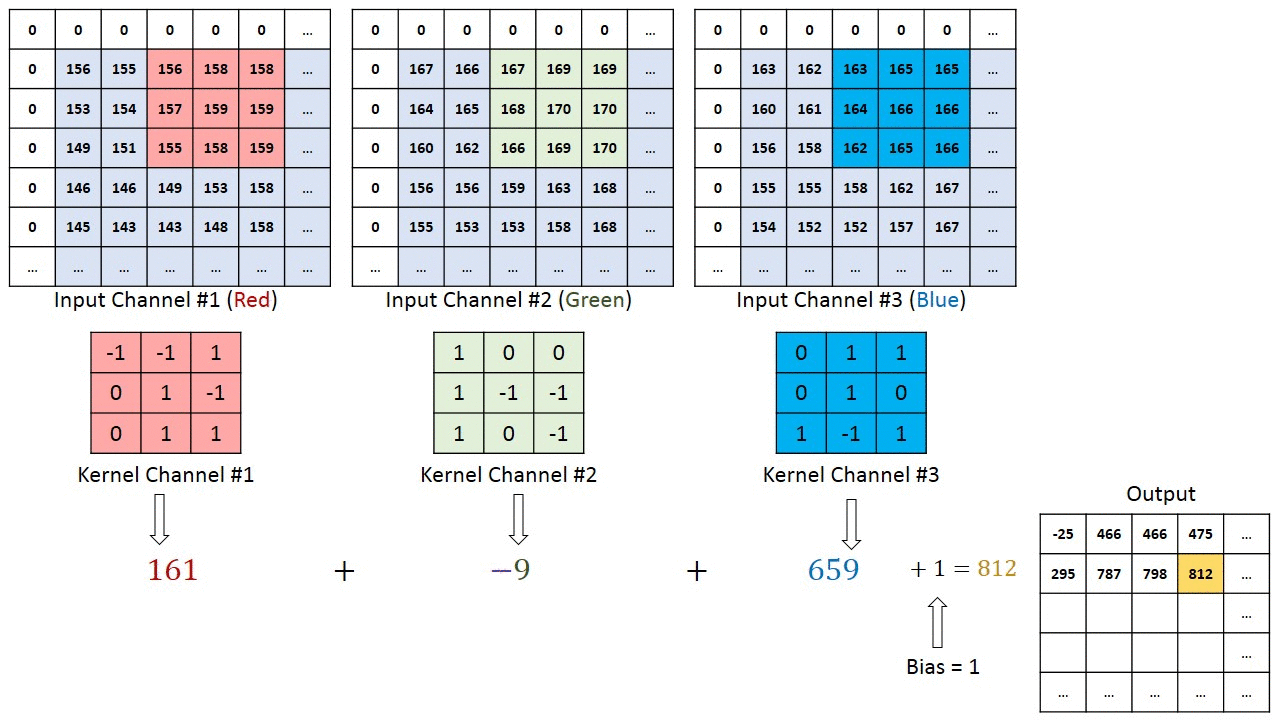
从上图可以知道,对于多通道的输入,卷积操作在每个Channel上分别进行,然后进行求和得到输出。比如,我的输入是$(32, W, H)$,我的输出是$(64, W, H)$,则需要新的卷积核的个数是$32 \times 64$。因为,对于在输入的32个通道的每个通道都需要64个卷积核,每个通道做完卷积运算,然后再求和,得到最后的64个通道的输出。
卷积运算的参数计算
根据前面的分析,到这里,卷积运算的参数的求解就很明确了。
设我们的输入通道是$p$,输出通道是$q$,则
如果我们不考虑Bias(增益),那么对于一个$m \times n$的卷积核(我们一般取$m =n$),我们需要学习的参数为$(m \times n \times p) \times q$;
如果加上Bias(就是给卷积核作用以后的结果添加一个常数),那么我们需要学习的参数为$(m \times n \times p + 1) \times q $。
逆卷积
在CNN中,我们经常会使用所谓的逆卷积(Decovolution)进行输入尺寸的放大,但是注意这个逆卷积不是卷积的逆操作。下面,我们还是看图说话,到底什么是逆卷积呢?(图中蓝色代表的是输入,青色代表的是输出)
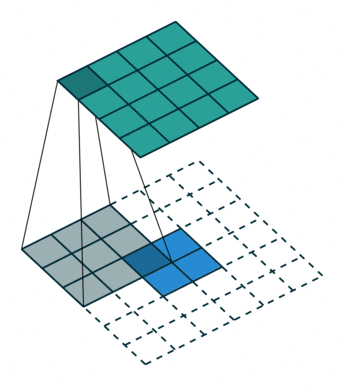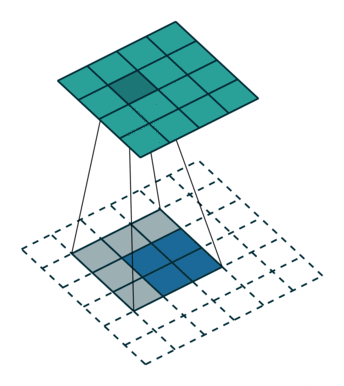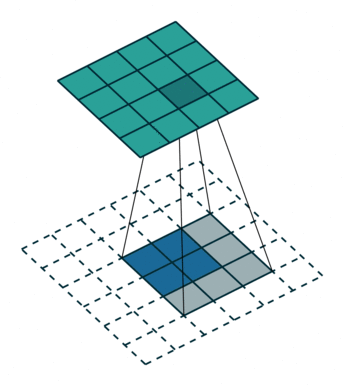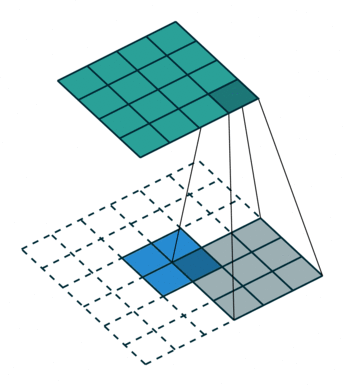
可以看到其实逆卷积和卷积操作并没有本质的区别,只是在输出的尺寸上有所区别。
卷积运算的矩阵实现
那么在计算机内部我们如何实现卷积操作呢?答案是矩阵乘法。
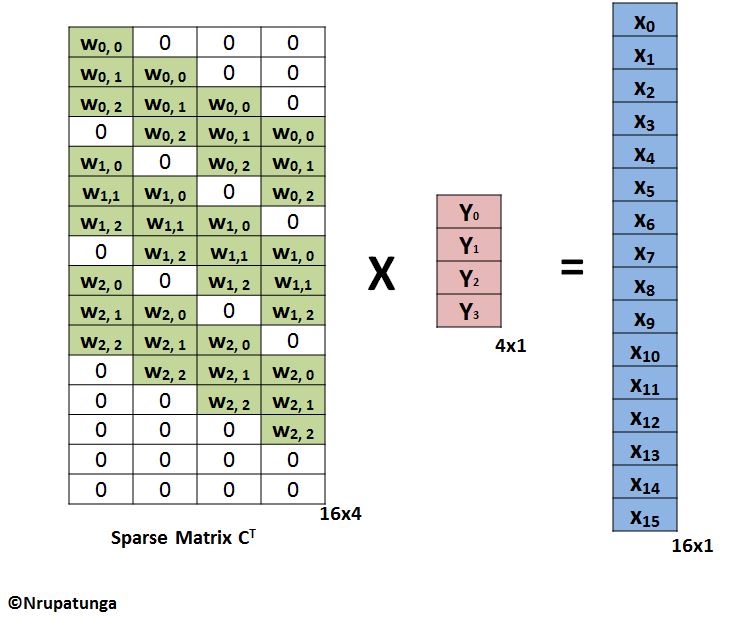
我们还是看图说话,对于卷积操作,我们对输入图像以及卷积核做Unroll操作以后,进行矩阵相乘得到输出。
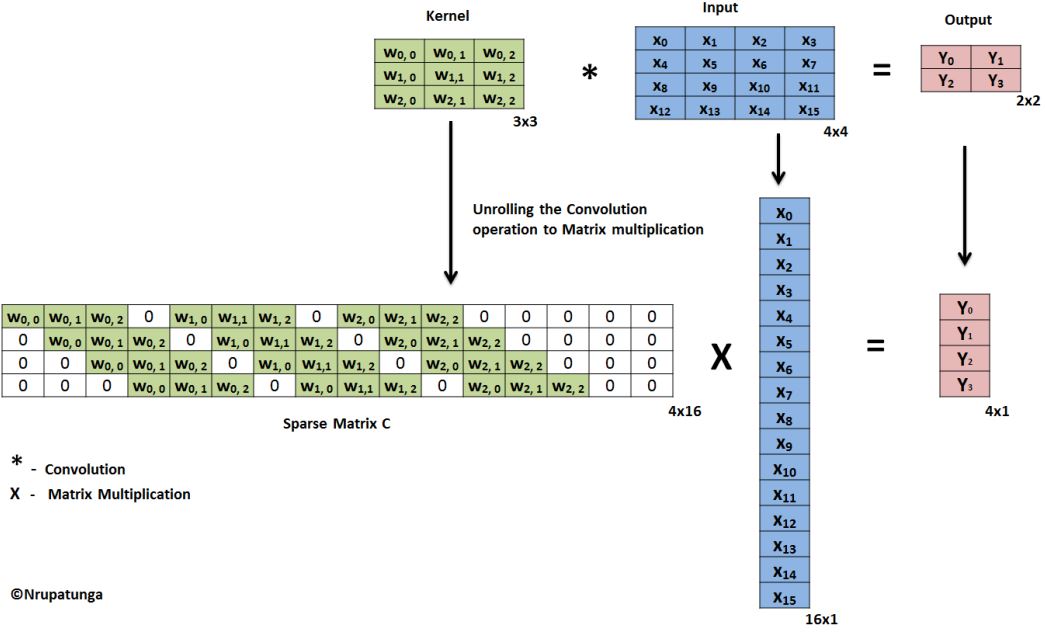
对于逆卷积操作,我们对卷积核进行Unroll操作以后进行转置,然后再做矩阵乘法,得到输入。所以基于这个原因,我们一般称逆卷积为转置卷积(Transposed Convolution)。