版权声明:本文为博主原创文章,转载请注明原文出处!
写作时间:2019-10-31
写这篇博文的初衷是在翻阅数字图像处理相关教科书的时候,发现大部分对傅立叶变换的讲解直接给出了变换公式,而对于公式从何而来并没有给出说明。所以,本文在假设已经了解傅立叶级数的背景下,从傅立叶级数推导出傅立叶变换的一般公式。
傅立叶级数
学过高数的童鞋都听过傅立叶级数,下面直接给出定义,具体证明可以参考高等数学教材。
设周期为$T$的周期函数$f(x)$的傅立叶级数为
$$f(x) = \frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos \frac{2\pi n x}{T}+b_{n} \sin \frac{2\pi n x}{T}\right) \tag{1}$$
其中,系数$a_n$和$b_n$分别为:
$$\left.\begin{array}{ll}{a_{n}=\frac{2}{T} \int_{\frac{T}{2}}^{\frac{T}{2}} f(x) \cos \frac{2\pi n x}{T} \mathrm{d} x} & {(n=0,1,2, \cdots)} \ {b_{n}=\frac{2}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \sin \frac{2\pi n x}{T} \mathrm{d} x} & {(n=1,2,3, \cdots)}\end{array}\right} \tag{2}$$
利用欧拉公式$$\cos t=\frac{\mathrm{e}^{t \mathrm{i}}+\mathrm{e}^{-t i}}{2}, \quad \sin t=\frac{\mathrm{e}^{t i}-\mathrm{e}^{-t i}}{2 \mathrm{i}}$$
可以将公式(1)转化为傅立叶级数的复数形式
$$f(x) = \sum\limits_{n=-\infty}^{\infty} c_{n} e^{\frac{2\pi n x}{T} \mathrm{i}} \tag{3}$$
系数$c_n$为
$$c_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \mathrm{e}^{-\frac{2\pi n x}{T} \mathrm{i}} \mathrm{d} x \quad(n=0, \pm 1, \pm 2, \cdots) \tag{4}$$
傅立叶级数的两种形式本质上是一样的,但是复数形式比较简洁,而且只用一个算式计算系数。
傅立叶变换
傅立叶级数是针对周期函数的,为了可以处理非周期函数,需要傅立叶变换。
傅立叶变换将周期函数在一个周期内的部分无限延拓,即让周期趋紧于无穷,然后就得到了傅立叶变换,如下图所示。
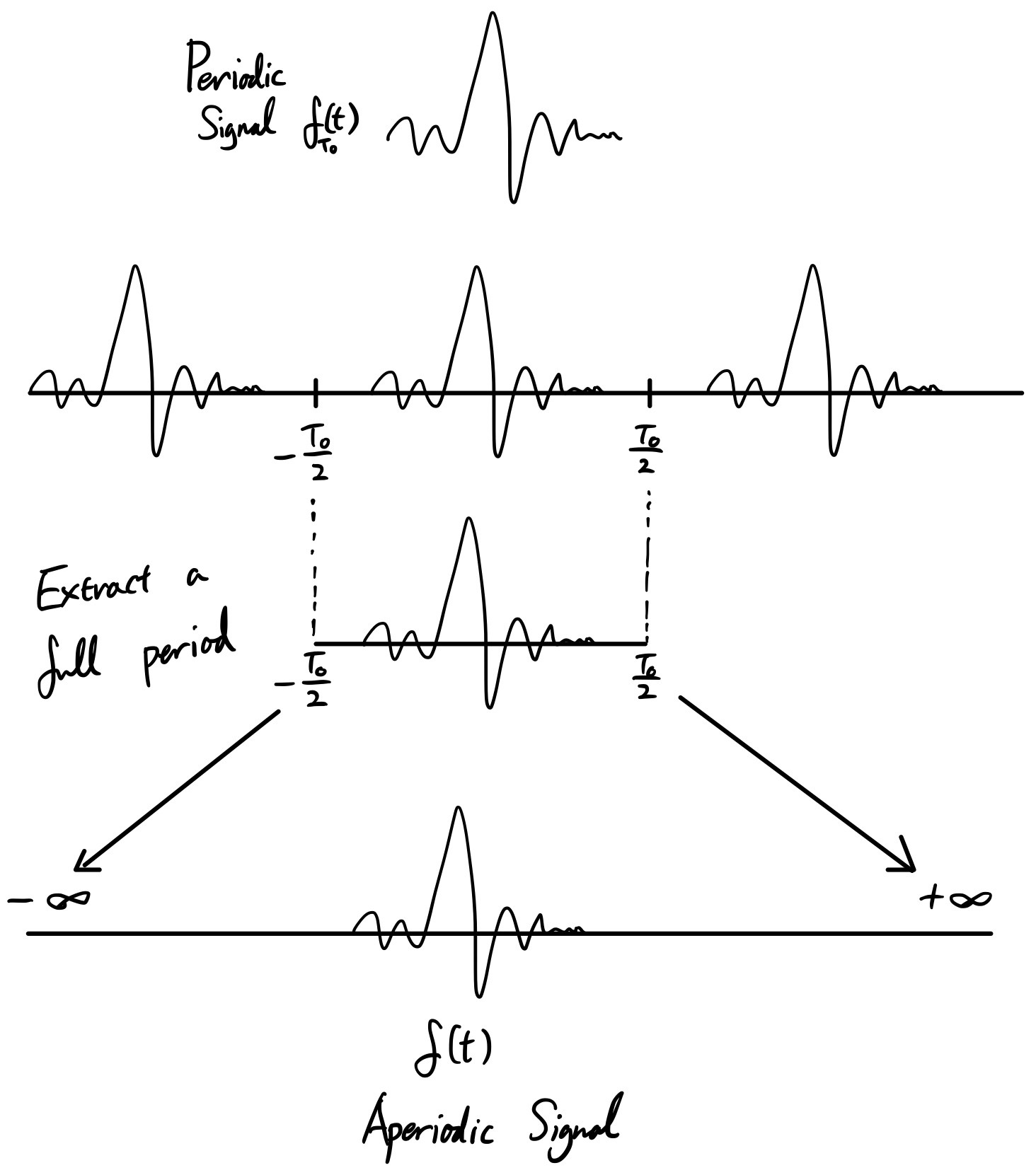
图片来源:Fourier Transform 101 — Part 3: Fourier Transform
下面我们看一下,当周期$T$趋于$\infty$的时候,我们看一下公式(3)和(4)的变化。
令$\frac{1}{T} = \Delta \omega$,则
$$\begin{align}f(x) &= \sum\limits_{n=-\infty}^{\infty} c_{n} e^{\frac{2 \pi n x}{T} \mathrm{i}} \ &= \sum\limits_{n=-\infty}^{\infty} c_{n} e^{2 \pi n \Delta \omega x \mathrm{i}} \ &= \sum\limits_{n=-\infty}^{\infty} \frac{1}{T} [\int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \mathrm{e}^{-2\pi n \Delta \omega x \mathrm{i}} \mathrm{d} x] e^{2 \pi n \Delta \omega x \mathrm{i}} \ \end{align}$$
当$T \to \infty$时,$\Delta \omega \to 0$,$\Delta \omega \to \mathrm{d}\omega$ ,$\mathrm{d}\omega$和$n \mathrm{d}\omega$都成为连续的变量,记为$\omega$。
$$\begin{align}f(x) &= \lim_{T\to \infty}{\sum\limits_{n=-\infty}^{\infty} \frac{1}{T} [\int_{-\frac{T}{2}}^{\frac{T}{2}} f(x) \mathrm{e}^{-n \pi xl \mathrm{i}} \mathrm{d} x] e^{2 \pi n \Delta \omega x \mathrm{i}}} \ &= \int_{-\infty}^{\infty}[\int_{-\infty}^{\infty}f(x)e^{-2\pi\omega x \mathrm{i}} \mathrm{d}x]e^{2\pi\omega x \mathrm{i}}\mathrm{d}\omega \ \end{align}$$
对应于傅立叶级数,傅立叶变换可以表示为
$$F(\omega) = \int_{-\infty}^{\infty}f(x)e^{-2\pi\omega x \mathrm{i}} \mathrm{d}x \tag{5}$$
而相应地傅立叶逆变换可以表示为
$$f(x) = \int_{-\infty}^{\infty}F(\omega) e^{2\pi\omega x \mathrm{i}}\mathrm{d}\omega \tag{6}$$