Python求解正态分布置信区间
正态分布和置信区间
正态分布(Normal Distribution)又叫高斯分布,是一种非常重要的概率分布。其概率密度函数的数学表达如下:
$$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x - \mu)^2}{2\sigma^2}}$$
当$\mu=0$,$\sigma = 1$时,称为标准正太分布。
置信区间是对该区间能包含未知参数的可置信的程度的描述。
使用SciPy求解置信区间
1 | import numpy as np |
输出如下:
1 | 0.0033541207210673997 0.9986647964318905 |
这里的-1.639303291798682是置信上界,1.6460115332408163是置信下界,两个数值构成的区间就是置信区间
使用Matplotlib绘制正态分布密度曲线
1 | # 绘制概率密度分布图 |
这里的pdf()函数是Probability density function,就是本文最开始的那个公式
最后的输出图像如下,可以看到结果跟理论上的正太分布还是比较像的:
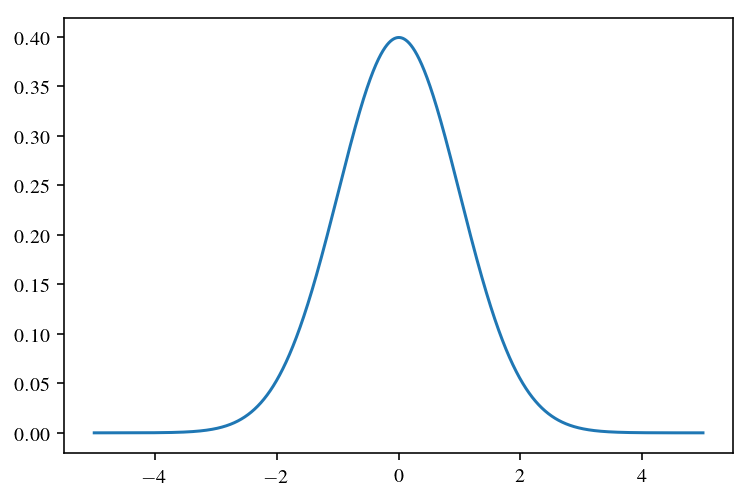
正态分布置信区间规律
函数曲线下68.268949%的面积在平均数左右的一个标准差范围内
函数曲线下95.449974%的面积在平均数左右两个标准差的范围内
函数曲线下99.730020%的面积在平均数左右三个标准差的范围内
函数曲线下99.993666%的面积在平均数左右四个标准差的范围内